Rounding Numbers in Microsoft® Excel, Access and VBA

Understanding the various forms of numerical rounding and how Microsoft Access, Excel and Visual Basic for Applications (VBA) deploy them.

Last updated on 2021-10-23 by David Wallis.

The Nature of Rounding

Consider the task of rounding a number that contains a fraction to, say, a whole number. The process of rounding in this circumstance is to determine which whole number best represents the number you are rounding.

In common, or arithmetic rounding, it is clear that 2.1, 2.2, 2.3 and 2.4 round to 2.0; and 2.6, 2.7, 2.8 and 2.9 to 3.0.

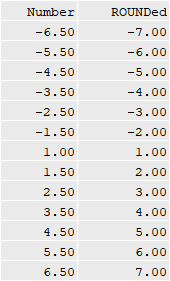
That leaves 2.5, which is no nearer to 2.0 than it is to 3.0. It is up to you to choose between 2.0 and 3.0, either would be equally valid.

To round 3.5, the Excel ROUND() function would choose 4.0:

For minus numbers under arithmetic rounding, -2.1, -2.2, -2.3 and -2.4, would become -2.0; and -2.6, 2.7, 2.8 and 2.9 would become -3.0 .

For -2.5, a choice is needed between -2.0 and -3.0. The Excel ROUND() function would choose -3.0.

Other Forms of Rounding

Rounding Up takes any number with decimal places and makes it the next “whole” number. Thus not only do 2.5 and 2.6 round to 3.0, but so do 2.1 and 2.2.

Rounding up moves both positive and negative numbers away from zero. E.g. 2.5 to 3.0 and -2.5 to -3.0.

Rounding Down truncates numbers by chopping off unwanted digits. This has the effect of moving numbers towards zero. E.g. 2.5 to 2.0 and -2.5 to -2.0

Banker’s Rounding — in its most common form — takes the .5 to be rounded and rounds it either up or down so that the result of the rounding is always an even number. Thus 2.5 rounds to 2.0, 3.5 to 4.0, 4.5 to 4.0, 5.5 to 6.0, and so on.

Alternate Rounding alternates the process for any .5 between rounding down and rounding up.

Random Rounding rounds a .5 up or down on an entirely random basis.

Symmetry and Asymmetry

A rounding function is said to be symmetric if it either rounds all numbers away from zero or rounds all numbers towards zero.

This is Excel’s ROUND() function performing symmetric rounding:

A function is asymmetric if it rounds positive numbers towards zero and negative numbers away from zero. Eg 2.5 to 2.0; and -2.5 to -3.0.

Also, asymmetric is any function that rounds positive numbers away from zero and negative numbers towards zero. Eg. 2.5 to 3.0; and -2.5 to -2.0.

Errors from Rounding

Any rounding introduces an error associated with the resulting rounded number. If you are rounding a series of numbers, then the overall accumulated error will usually skew your result:

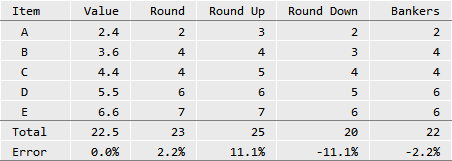
You might choose to use banker’s rounding in your attempts to balance out the effect of rounding errors, thereby reducing the skew.

Random rounding is another way of attempting to offset the skew.

Note: You should not assume that random rounding necessarily gives less error than banker’s, or alternate, rounding.

Also, there is the consideration that random rounding may give different results for the same set of figures.

Excel Rounding Functions

Excel’s ROUND() function performs arithmetic rounding and is symmetric. It rounds numbers up and in so doing moves them away from zero, e.g. ROUND() rounds -2.5 to -3.0.

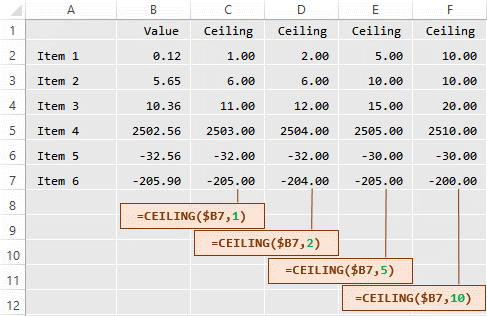
CEILING() rounds a number to the nearest multiple of a significant number of your choice. In doing so it moves positive numbers away from zero, and negative numbers towards zero:

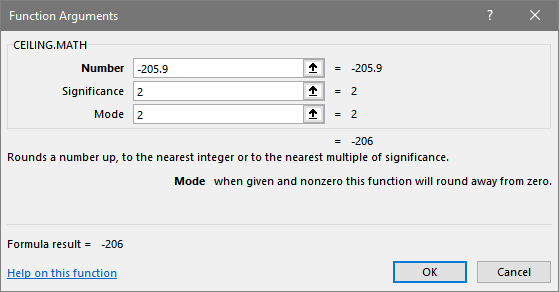
CEILING.MATH() rounds a number to the nearest multiple of a significant number of your choice. Additionally, by way of its Mode argument CEILING.MATH() allows you to choose between rounding towards, or away from, zero:

ROUNDDOWN() round numbers down and in so doing move them towards zero. Eg Excel rounds down -2.5 to -2.0.

FLOOR() moves the result in the opposite direction to CEILING():

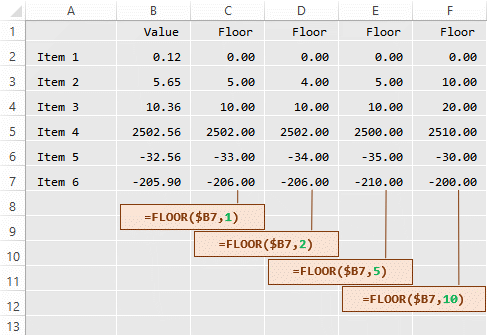
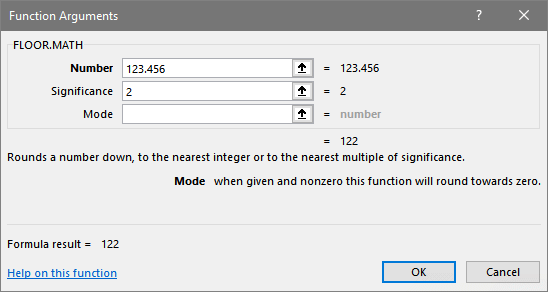
FLOOR.MATH() rounds down, and like CEILING.MATH() offers you choice of rounding towards, or away from, zero:

The INT() function moves positive numbers towards zero, and negative numbers away from zero, as it rounds a number to the nearest whole-number (integer) equivalent.

You use the FIXED() function to return a number as text. In making the conversion the function rounds in the same way as ROUND().

You may find MROUND() easier to use than ROUND() for certain calculations, as the Microsoft Excel ROUND and MROUND Functions to Round to Nearest 5 page illustrates.

As far as I know, there are no functions in Excel for either alternate, banker’s or random rounding.

Rounding in Access and VBA

Excel-like Rounding in Access has details of my custom function that brings Excel-like rounding to Access/VBA..

VBA’s Int() function behaves in the same way as Excel’s INT().

VBA’s Fix() function behaves like Int() for positive numbers; but when applied to a negative number it rounds towards zero.

There are no functions in VBA for alternate or random rounding, so far as I’m is aware.

Your Support for DMW TIPS

Please support this website by making a donation to help keep it free of advertising and to help towards cost of time spent adding new content.

To make a contribution by PayPal in GBP (£ sterling) —

To make a contribution by PayPal in USD ($ US) —

Thanks, in anticipation.